목차
문제 출처 : https://www.acmicpc.net/problem/17610
17610번: 양팔저울
무게가 서로 다른 k개의 추와 빈 그릇이 있다. 모든 추의 무게는 정수이고, 그릇의 무게는 0으로 간주한다. 양팔저울을 한 번만 이용하여 원하는 무게의 물을 그릇에 담고자 한다. 주어진 모든 추
www.acmicpc.net
이 문제는 2019년 정보 올림피아드 1차 중등부 1번 문제 입니다.
양팔 저울을 가지고 만들 수 있는 모든 무게를 찾아 불가능한 경우의 수를 출력하는 문제 입니다. 따라서 1부터 모든 추의 무게를 따져가며 만들 수 있는지, 없는지 확인해야 합니다.
이런 문제는 DP를 통해 풀 수 있습니다. DP의 배낭 문제를 통해 이 문제의 해결 방안을 생각해 볼 수 있습니다. 경우의 수를 따져가며 Top - Down 방식으로 문제를 해결해 보겠습니다. 배낭 문제에 대해 잘 모른다면 아래 링크를 확인 부탁 드립니다.
02. 배낭 문제
배낭 문제(Knapsack Problem)는 배낭안에 물건을 채우는 방법에 대한 문제 입니다. 그냥 물건을 채우는 것이 아니라 가치가 다른 물건들을 잘 조합하여 최대의 가치를 가…
wikidocs.net
이 문제에서 무게를 만드는 방법은 3가지가 있습니다. 어떤 무게의 추를 왼쪽 저울에 둘지, 오른쪽 저울에 둘지, 어떤 저울에도 올리지 않을지 입니다.
문제 이해하기
가령 예제에 있는 저울들로 6의 무게를 측정하는 방법을 생각해 보겠습니다.
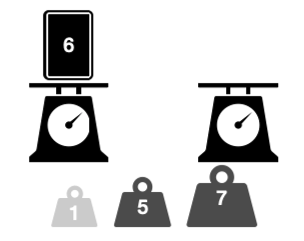
1의 추를 왼쪽에 넣거나, 오른쪽에 넣거나, 아예 넣지 않는 3가지 경우를 생각해 보겠습니다.
먼저 왼쪽에 1의 추를 넣는 경우 오른쪽에 7의 추를 넣으면 양쪽 모두 무게가 7이 되어 측정이 가능 합니다.

반대로 오른쪽에 추를 넣으면 5의 추를 오른쪽에 추가하여 양쪽 모두 무게가 6이 되어 측정이 가능합니다.

마지막으로 1의 추를 넣지 않으면 5와 7로는 6을 만들 방법이 없어 측정이 불가능 합니다.
이렇게 3가지 경우를 생각하며 DP로 원하는 결과를 얻을 수 있습니다.
코드 작성
그럼 코드를 작성해 보겠습니다.
입력 받기
k = int(input())
weight = list(map(int, input().split()))
추의 개수 k와 무게들인 weight를 입력 받았습니다.
초기화 하기
S = sum(weight)
dp = [False] * (S+1)
다음으로 우리가 구할 수 있는 최대 무게를 구해줍니다. 아무리 추를 놓아도 전체 무게 이상을 젤 수는 없습니다. 문제에서는 추 무게의 합을 S라 하였기에 똑같이 S로 하였습니다. 그리고 우리가 구해야 하는 것은 해당 무게를 젤수 있는지, 없는지 입니다. 그것을 확인할 배열 dp를 처음에는 젤수 없다는 뜻으로 False로 초기화 하였습니다.
결과 출력하기
solve(0, 0)
ans = 0
for chk in dp[1:]:
if not chk:
ans += 1
print(ans)
solve란 함수를 통해 모든 무게를 체크할 것입니다. solve 함수 만드는 것은 결과 출력 부분 설명 이후에 진행하겠습니다. solve 함수를 통해 dp 리스트에는 해당 무게를 젤 수 있으면 True, 젤 수 없으면 False가 들어있게 됩니다. 무게 1부터 확인하여 False가 있는 경우 ans 값을 1씩 늘려주고 그 값을 출력하면 측정이 불가능한 경우의 수가 됩니다.
solve 함수
이 문제의 핵심이라 할 수 있는 solve 함수를 알아보겠습니다.
def solve(i, w):
solve(i + 1, w + weight[i])
solve(i + 1, w - weight[i])
solve(i + 1, w)
먼저 solve 함수에 들어가는 인자 입니다. i는 추의 순서 입니다. i번째 추를 왼쪽에 올릴지, 오른쪽에 올릴지, 올리지 않을지를 정하는 것입니다. w는 현재의 무게 입니다. 결과 출력하기에서 0번째 추로 아무것도 올리지 않은 무게인 0부터 확인하기 위해 solve(0, 0)으로 시작한 것입니다.
추가 오른쪽에 놓이면 원래 무게 w에 추의 무게를 더해주어야 합니다. 그래서 w + weight[i]가 된 것입니다. 추가 왼쪽에 놓인다는 것은 추가 있는 오른쪽 w의 무게에 weight[i]를 빼준 것과 같습니다. 마지막으로 추를 추가하지 않는 것은 w 그대로 놓인 것과 같습니다.
Top-Down으로 문제를 해결할 때에는 종료조건이 필수적으로 있어야 합니다. 종료 조건을 추가해 보겠습니다.
종료 조건 추가하기
종료가 되는 경우는 모든 추를 다 사용했을 때 입니다. 추를 추가하지 않은 결정 조차도 추를 사용했다고 생각하는 것입니다.
def solve(i, w):
if i == k:
if 0 < w <= S:
dp[w] = True
else:
solve(i + 1, w + weight[i])
solve(i + 1, w - weight[i])
solve(i + 1, w)
추를 모두 사용했다는 것은 i의 값이 추의 개수인 k와 같아질 때 입니다. k개의 추를 모두 고려했을 때 만들 수 있는 무게 w에 대해 True로 바꿔준 것입니다. 이 때 w의 무게는 음수가 나올수도 있습니다. 왜냐하면 w - weight[i]쪽으로 모든 추가 들어갔다면 -S값이 될 것이고, 이것은 우리가 구하려는 추의 무게에 없기 때문 입니다.
그래서 추의 무게 범위를 0보다 크고, S보다는 작거나 같도록 해주었습니다. 이렇게 모든 무게를 확인하면 측정 불가능한 경우의 수를 확인할 수 있습니다.
전체 코드
전체 코드를 확인해 보겠습니다.
k = int(input())
weight = list(map(int, input().split()))
S = sum(weight)
dp = [False] * (S+1)
def solve(i, w):
if i == k:
if 0 < w <= S:
dp[w] = True
else:
solve(i + 1, w + weight[i])
solve(i + 1, w - weight[i])
solve(i + 1, w)
solve(0, 0)
ans = 0
for chk in dp[1:]:
if not chk:
ans += 1
print(ans)
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 17611] 2019 정올 1차 중등부 2번 "직각다각형" (2) | 2024.03.01 |
|---|---|
| [백준 17613] 2019 정올 1차 고등부 "점프" (0) | 2024.02.29 |
| [백준 17612] 2019 정올 1차 고등부 "쇼핑몰" (0) | 2024.02.22 |
| [백준 17609] 2019 정올 초등부 1차 "회문" (2) | 2024.02.20 |
| [백준 28323] 2023 정올 2차 초등부 "불안정한 수열" (0) | 2024.02.19 |


