목차
문제 출처 : 주유소
2023년도 정보올림피아드에도 주유소란 이름의 문제가 있어 혼란스러울 수 있으나 두 문제는 다른 문제 입니다. 2023년도 주유소 문제는 아래 링크에서 확인 가능 합니다.
https://davincicoding.tistory.com/9
[백준 28219] 2023 정올 1차 주유소
문제 출처 : https://www.acmicpc.net/problem/28219 28219번: 주유소 KOI 국가는 $N$개의 마을로 이루어져 있다. 각 마을에는 $1$번 마을, $2$번 마을, $\cdots$, $N$번 마을과 같이 번호가 붙어 있다. 그리고 도로가 $
davincicoding.co.kr
2016년도 주유소 문제는 다익스트라 알고리즘으로 해결할 수 있는 문제 입니다. 다만 문제가 기름을 어디서 넣느냐에 따라 비용이 변경된다는 점 입니다. 따라서 최대한 저렴한 기름으로 이동을 해야 최소 비용을 만들 수 있습니다. 기름값을 비교하여 저렴한 기름값이 등장하면 다음 노드부터는 저렴한 기름값으로 이동하도록 로직을 구성해야 합니다.
문제 이해하기
다음으로 문제에 예제로 보여준 내용을 잘 이해해야 합니다.

1에서 4까지 이동할 때 위 그림처럼 이동한다면 5 * 3 + 4 * 4로 31이라는 비용이 듭니다. 이것보다 더 비용을 절약하는 방법은 아래 그림처럼 이동하는 것입니다.
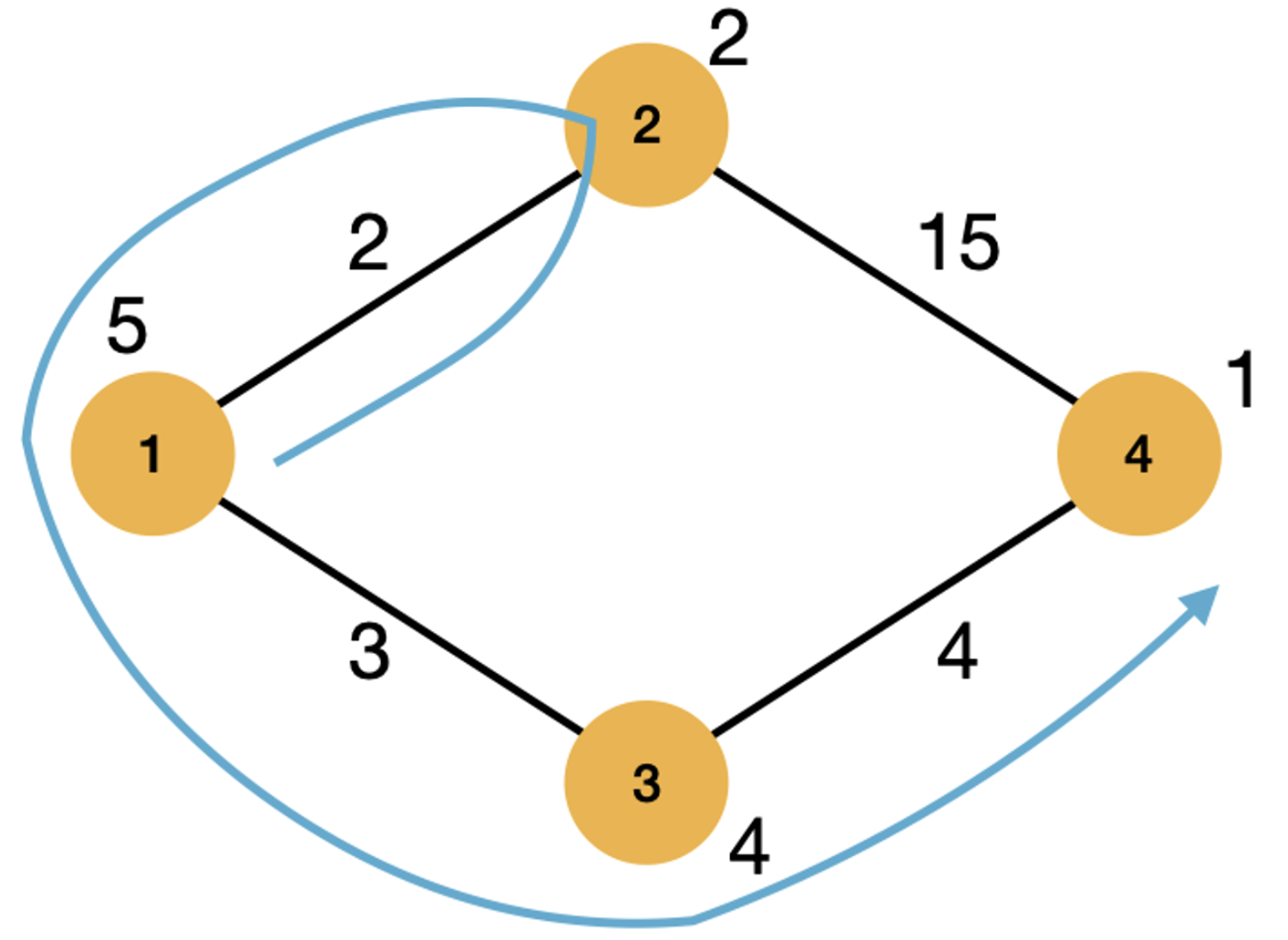
1에서 2로 이동하여 2번 도시에 있는 싼 기름값을 넣고 그 기름으로 다시 1, 3, 4로 가는 것입니다. 이렇게 이동하면 5 * 2 + 2 * 2 + 3 * 2 + 4 * 2로 10 + 4 + 6 + 8 = 28이 되어 28의 비용으로 이동할 수 있습니다. 즉 거리는 더 길어졌을지 몰라도 싼 기름으로 이동할 수 있는 것입니다.
이로인해 지금까지 계산하던 방식과는 다르게 거리를 계산해야 합니다. 1번의 경우 처음 시작 지점이기 때문에 거리가 0입니다. 이 0이라는 숫자는 가장 작은 숫자로 더 짧은 숫자로 변경이 불가능 합니다. 이것을 해결하기 위해 도시로만 거리를 측정하는 것이 아니라 어떤 기름으로 도착했는지를 기억하도록 변경해야 합니다.
코드 작성하기
그럼 문제를 직접 풀어보도록 하겠습니다.
입력 받기
mii = lambda : map(int, input().split())
N, M = mii()
oil = [0] + list(mii())
arr = [[] for _ in range(N + 1)]
for _ in range(M):
u, v, w = mii()
arr[u].append((w, v))
arr[v].append((w, u))
먼저 도시의 수 N과 도로의 수 M을 입력 받습니다. 다음으로 기름값을 입력 받습니다. 이 때 도시의 번호와 기름의 번호가 일치할 수 있도록 0번째 기름 0을 추가하였습니다.
그리고 각각의 도시들과 도시를 잇는 도로의 길이를 입력 받습니다. 도로에는 방향이 없기 때문에 양쪽 모두 이동이 가능하도록 입력합니다. 저는 도로의 길이 w와 도착 도시 u나 v를 입력 받도록 하였습니다. 이는 다익스트라 알고리즘에서 우선순위 큐를 사용하는데 큐에서는 거리를 먼저 받고, 도시들은 도시 번호를 먼저 받는 것을 매번 신경써야 해서 이를 하나로 통일 시키기 위해 거리를 먼저 입력 받도록 한 것입니다.
다익스트라 시작값 지정하기
def dijkstra():
INF = float("INF")
price = [[INF] * (N + 1) for _ in range(N + 1)]
q = [(0, 1, 1)]
다익스트라 알고리즘의 시작 부분 입니다. 그동한 비용은 1차원 배열로 만들었지만 여기서는 2차원 배열로 만들어 주었습니다. 왜냐하면 위에서도 언급했듯이 이미 지나갔던 도로를 더 싼 기름을 넣고 다시 돌아올 수 있기 때문 입니다. 그리고 큐에는 시작 위치의 거리 0, 시작 도시 1번, 넣은 기름의 도시 1을 넣었습니다.
다익스트라 반복문
while q:
cur_price, cur_node, oil_node = heappop(q)
if cur_node == N:
return cur_price
for nxt_dist, nxt_node in arr[cur_node]:
new_price = cur_price + oil[oil_node] * nxt_dist
if new_price < price[nxt_node][oil_node]:
price[nxt_node][oil_node] = new_price
new_oil_node = oil_node
if oil[nxt_node] < oil[oil_node]:
new_oil_node = nxt_node
heappush(q, (new_price, nxt_node, new_oil_node))
반복문 부분 입니다. 지금까지의 다익스트라와 비슷하면서도 다릅니다. 가장 다른 부분은 기름값으로 인해 비용 계산하는 방식이 다릅니다. 기존 거리는 다음과 같은 방식으로 계산 하였습니다.
distance = cur_dist + nxt_dist
이렇게 계산하였지만 여기서는 기름값에 따라 그 값이 달라지기 때문에 기름값으로 계산하도록 하였습니다.
new_price = cur_price + oil[oil_node] * nxt_dist
다음으로 비용을 업데이트 하기 위해서 비교하는 부분 입니다. 여기서는 어떤 기름으로 이동했느냐에 따라 값이 달라지기 때문에 비교 구문이 아래와 같이 변경 되었습니다.
if new_price < price[nxt_node][oil_node]:
price[nxt_node][oil_node] = new_price
거리가 업데이트 될 때는 다음 도시의 기름값과 비교합니다. 새로운 도시의 기름값이 싸다면 그 값으로 바꿔주어야 합니다. 그리고 그 값을 큐에 넘겨주어 다음부터는 싼 기름으로 이동할 수 있게 합니다.
new_oil_node = oil_node
if oil[nxt_node] < oil[oil_node]:
new_oil_node = nxt_node
heappush(q, (new_price, nxt_node, new_oil_node))
마지막으로 다익스트라 알고리즘에서 나온 비용을 출력하면 됩니다.
전체 코드
그럼 전체 코드를 확인해 보겠습니다.
from heapq import heappop, heappush
mii = lambda : map(int, input().split())
N, M = mii()
oil = [0] + list(mii())
arr = [[] for _ in range(N + 1)]
for _ in range(M):
u, v, w = mii()
arr[u].append((w, v))
arr[v].append((w, u))
def dijkstra():
INF = float("INF")
price = [[INF] * (N + 1) for _ in range(N + 1)]
q = [(0, 1, 1)]
while q:
cur_price, cur_node, oil_node = heappop(q)
if cur_node == N:
return cur_price
for nxt_dist, nxt_node in arr[cur_node]:
new_price = cur_price + oil[oil_node] * nxt_dist
if new_price < price[nxt_node][oil_node]:
price[nxt_node][oil_node] = new_price
new_oil_node = oil_node
if oil[nxt_node] < oil[oil_node]:
new_oil_node = nxt_node
heappush(q, (new_price, nxt_node, new_oil_node))
print(dijkstra())
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 11779] 최소 비용 구하기 2 (3) | 2024.01.23 |
|---|---|
| [백준 10844] 쉬운 계단 수 (1) | 2024.01.22 |
| [백준 1219] 오민식의 고민 (1) | 2024.01.01 |
| [백준 1865] 웜홀 - 플로이드 워셜 풀이 (1) | 2023.12.17 |
| [백준 1504] 특정한 최단 경로 (0) | 2023.12.09 |


