목차
문제 출처 : https://www.acmicpc.net/problem/22344
22344번: 그래프 균형 맞추기
N개의 정점과 M개의 간선으로 구성된 무방향 단순 연결 그래프가 있다. 그래프의 정점들에는 1 이상 N 이하의 서로 다른 자연수 번호가 붙어 있고, 간선들에는 1 이상 M 이하의 서로 다른 자연수
www.acmicpc.net
이 문제는 2021년 정보올림피아드 2차 초등부, 고등부 문제 입니다.
초등부 문제이지만 고등부에서도 출제된 문제인 만큼 쉽지 않은 문제 입니다. 문제 자체를 이해하는건 어렵지 않습니다. 간선의 가중치가 있고, 간선과 이어진 두 정점의 합이 간선의 가중치가 되면 됩니다. 예제 입력을 보면서 이해해 보겠습니다.

정점 1, 2, 3을 값과의 혼란을 피하기 위해 A, B, C로 바꿔주었습니다. 이제 간선의 값을 통해 이러한 공식을 만들 수 있습니다.
A + B = 5, B + C = 4, C + A = 3
모든 식을 합하면 다음과 같은 식을 구할 수 있습니다.
2(A + B + C) = 5 + 4 + 3
A + B + C = 6
이것으로 A, B, C의 값을 구할 수 있습니다.
A = 2, B = 3, C =1
만약 식이 성립하지 않거나, 계산 결과에 실수가 나온다면 더 이상 따져볼 것도 없이 No를 출력하면 됩니다.
이것이 서브테스크 1번으로 문제가 너무 어렵다면 부분점수 6점을 얻는것으로 해볼 수 있습니다.
서브테스크 1
서브테스크1은 이미 모든 노드가 정해져 있습니다. 따라서 위 공식으로 코드를 작성할 수 있습니다.
입력 받기
N, M = map(int, input().split())
arr = [[0] * (N+1) for _ in range(N+1)]
for _ in range(M):
a, b, c = map(int, input().split())
arr[a][b] = c
arr[b][a] = c
입력을 인접행렬 형태로 받습니다. 왜냐하면 이미 우리가 구해야할 값을 알고 있기 때문에 굳이 어렵게 리스트 형태로 받을 필요가 없습니다.
계산하기
total = arr[1][2] + arr[2][3] + arr[3][1]
if total % 2 == 1:
print("No")
else:
print("Yes")
half = total // 2
node_a = half - arr[2][3]
node_b = half - arr[1][3]
node_c = half - arr[1][2]
print(node_a, node_b, node_c
간선들의 가중치를 모두 더하면 A+B+C 값의 2배입니다. 이 값이 2의 배수가 아니라면 정점의 값이 정수일 수 없습니다. 따라서 total 값이 2의 배수가 아니면 무조건 No를 출력해 줍니다.
2의 배수라면 위 공식을 이용하여 node의 값을 구할 수 있습니다. 먼저 total 값을 2로 나누어 A+B+C의 값을 구합니다. 그 값을 half라 하였습니다. 다음으로 A정점의 값을 구하기 위해서는 half에서 BC간선의 가중치를 빼줍니다. 그렇게 node_a의 값을 구한 것입니다. 같은 방식으로 B, C 정점의 값을 구해 출력해 주면 됩니다.
서브테스트2
서브테스트2의 의미를 잘 살펴보면 일직선의 리스트를 나타낸 것입니다. j번 간선은 j번 정점과 j+1번 정점을 잇고 있기 때문에 일렬로 늘어진 리스트를 생각할 수 있습니다.

이런 모양이 되고, 정점의 값은 정해지지 않고 많은 케이스가 존재합니다. 여기서 만약 A가 0이면 B는 1이 되고, C는 -4가 되고, D는 9가 됩니다. 또는 A값이 1이 되면 B는 0이 되고, C는 -3이 되고, D는 8이 됩니다. 이렇게 여러 형태의 답을 가질 수 있기 때문에 각 정점들의 값의 절대값의 합이 최소가 되는 경우를 찾는 것입니다.
A가 0일때의 값은 0 + 1 + |-4| + 9로 14가 됩니다. A가 1일때는 1 + 0 + |-3| + 8로 12가 됩니다. 여러가지 케이스를 구해보면 A가 1일 때가 최소값이 됩니다. 그럼 이것을 식으로 나타내 보겠습니다.
A값을 x라고 했을 때 B는 1 - x가 됩니다. C는 -3 - (1 - x)가 되고, D는 5 -(-3 - (1 - x))가 됩니다.
A = x, B = 1 - x, C = -4 + x, D = 9 - x
A, B, C, D정점의 절대값의 최소값을 구하는 식은 다음과 같습니다.
|x| + |1 - x| + |x - 4| + |9 - x|
우리는 절대값을 구하는 것이기 때문에 모든 식을 x - a 형태로 바꿔주었습니다. 이제 이 식이 최소가 되는 경우가 답이 됩니다. 어느 정점인지 모르지만 어떤 정점이 0이 될 때 최소값을 갖기 때문에 정점이 0이되는 경우를 계산하면 답을 구할 수 있습니다.
입력 받기
N, M = map(int, input().split())
arr = [[] for _ in range(N+1)]
for _ in range(M):
a, b, c = map(int, input().split())
arr[a].append((b, c))
arr[b].append((a, c))
서브테스크1과는 다르게 인접리스트 형태로 입력을 받습니다. 일렬로된 리스트를 받기 때문에 인접 행렬 형태는 비효율적입니다.
가중치를 구하는 함수 만들기
cost = [0] * (N+1)
def dfs(node, node_cost, a):
visited[node] = True
cost[node] = (a, node_cost)
for nxt, edge_cost in arr[node]:
if visited[nxt]:
continue
dfs(nxt, edge_cost - node_cost, -a)
visited = [False] * (N+1)
dfs(1, 0, 1)
dfs를 사용하여 가중치를 구하는 함수를 만들었습니다. 우리가 알고 있는 간선의 가중치를 통해 정점의 가중치를 구해줍니다. 1번 노드의 가중치를 0으로 하여 각 노드들의 가중치를 구해줍니다. 간선의 가중치 edge_cost를 알고 있기 때문에 노드의 가중치 node_cost를 빼면 다음 노드의 가중치를 알 수 있습니다.
a값은 가중치의 부호입니다. 위 예제에서 각 노드들의 가중치를 보면 다음과 같습니다.
A = x, B = 1 - x, C = -4 + x, D = 9 - x
x값이 A는 +x, B는 -x, C는 +x, D는 -x로 부호가 노드의 순서에 따라 계속 바뀝니다. 초기값이 0이기 때문에 이 부호를 기억하기 위해서 a라는 값으로 넘겨주는 것입니다. 그렇기에 dfs를 돌릴 때 -a로 계속 부호를 바꿔주는 것입니다.
이렇게 하면 cost라는 리스트에 부호와 가중치값이 들어있게 됩니다. 위 예제를 돌려보면 cost 리스트에는 다음과 같은 값이 들어 있게 됩니다.
[0, (1, 0), (-1, 1), (1, -4), (-1, 9)]
0번째는 0으로 사용하지 않습니다. 첫 번째 값 (1, 0)은 부호는 +이고, 가중치값이 0을 뜻합니다. 1 * x + 0을 뜻하는 것으로 A = x를 뜻합니다.
두 번째 값 (-1, 1)은 부호는 -, 가중치는 1로 B = -1 * x + 1을 뜻합니다. 즉 위에서 구한 B = 1 - x와 같은 형태가 됩니다. C 역시 부호와 가중치 (1, -4)를 통해 -4 + x를 구할 수 있습니다.
cost 리스트를 통해 위에서 보았던 A, B, C, D의 식을 만든 것입니다.
비용의 최소값 구하기
def get_weight(x):
total = 0
for a, c in cost[1:]:
temp = a * x + c
if temp < 0:
temp *= -1
total += temp
return total
rst = float("INF")
x = 0
for a, c in cost[1:]:
ac = -a * c
tmp = get_weight(ac)
if tmp < rst:
rst = tmp
x = ac
cost 리스트를 통해 정점의 식을 구했기 때문에 총 비용의 최소값을 구할 수 있습니다. 총 비용의 최소값은 정점의 값을 0으로 만드는 값 중 하나이기 때문에 -a * c를 통해 구할 수 있습니다. 첫 번째 값인 -1 * 0을 통해 A 정점을 0으로 만들어서 비용의 값을 구해보고, 다음 값인 -(-1) * 1인 1로 두번째 값을 1 - 1 = 0으로 만들 수 있습니다. 이값으로 get_weight 함수에 x값을 하면 총 비용을 구할 수 있습니다. 우리가 구하는 총 비용은 절대값이기 때문에 temp값이 0보다 작으면 -1을 곱해 양수로 만들어 줍니다. 총 비용 total값을 구해 리턴해 줍니다.
모든 정점을 통해 총 비용을 구하면서 최소값을 찾습니다. 그리고 총 비용의 최소값일때의 x값을 기록해 놓습니다.
정점 값 출력하기
print("Yes")
for a, c in cost[1:]:
print(a * x + c, end=" ")
print()
출력형식을 보면 먼저 Yes나 No를 출력합니다. 우리는 지금 서브테스트2를 해결하기 위한 것으로 어떤 경우에도 정점을 구할 수 있습니다. x값에 따라 정점의 값이 달라질 뿐이지 리스트를 만들 수 없는 경우는 없기 때문입니다. 그래서 가능 여부를 따지지 않고 Yes를 그냥 출력합니다. 다음으로 cost를 통해 각 정점의 값을 출력합니다. x 값을 알기 때문에 계산을 통해 각 정점값을 출력할 수 있습니다.
이것으로 서브테스크2를 해결할 수 있습니다.
서브테스크3
서브테스크3은 서브테스크2와 똑같은 조건입니다. 다만 N의 크기의 제약이 사라졌습니다. 따라서 좀 더 빠른 알고리즘을 생각해야 합니다. 이 문제의 총 비용은 절대값을 통해 만들어 집니다. 따라서 절대값의 특징을 알면 알고리즘을 좀 더 빠르게 만들 수 있습니다.
|x| + |1 - x| + |x - 4| + |9 - x|
예제를 통해 비용을 구하는 함수를 그려보겠습니다. 먼저 |x|의 그래프 입니다.

절대값 그래프이기 때문에 x값이 0이되는 0을 기준으로 V형태의 그래프를 가지게 됩니다. 다음으로 |1 - x|를 추가해 보겠습니다.

|x| + |1 - x| 그래프는 0과 1사이가 최소값이 되는 것을 알 수 있습니다. 다음으로 |x - 4|를 추가하겠습니다.

|x| + |1 - x| + |x - 4|는 1일때 최소값임을 알 수 있습니다. 마지막으로 |9 - x| 를 추가해 주겠습니다.

|x| + |1 - x| + |x - 4| + |9 - x| 의 최소값은 1부터 4사이의 값이 되었습니다. 지금까지를 통해 알 수 있는 것은 정점들이 0이될 때를 모두 확인할 필요가 없습니다. 그래프가 U 형태이기 때문에 중간값이 바로 최소값이라는 것을 알 수 있습니다. 처음에는 0이 최소값이였다가, 다음에는 0과 1사이, 다음에는 1, 다음에는 1과 4사이로 정점들의 중간값을 찾으면 각 정점들의 총 비용을 구할 필요없습니다.
중간값으로 최소 비용 찾기
cost = [0] * (N+1)
weight = [0] * (N+1)
def dfs(node, node_cost, a):
visited[node] = True
cost[node] = (a, node_cost)
weight[node] = -a * node_cost
for nxt, edge_cost in arr[node]:
if visited[nxt]:
continue
dfs(nxt, edge_cost - node_cost, -a)
visited = [False] * (N+1)
dfs(1, 0, 1)
weight.sort()
x = weight[(N+1) // 2]
weight라는 리스트를 추가해 주었습니다. 가중치의 중간값을 찾기위한 것입니다. weight값을 정렬하여 중간값을 통해 x를 찾으면 매번 총 비용을 구하지 않고도 답을 구할 수 있습니다.
이 소스를 제출하면 서브테스크3과 4를 해결할 수 있습니다. 서브테스크4를 의도한 것은 아니었지만 문제가 해결된 것입니다. 서브테스크4는 j번 정점과 j+1번 정점을 잇는다는 부분이 빠져있습니다. 이 말은 일렬로 이어진 것이 아닌 트리형태라는 뜻입니다. N-1개의 간선으로 정점들을 모두 연결하기 위해서는 트리형태밖에 없기 때문입니다.
서브테스크5
서브테스크5는 M과 N의 수가 같습니다. 이 조건의 뜻은 사이클이 형성되어 있다는 뜻입니다. 서브테스크1처럼 처음 정점과 마지막 정점을 연결하면 M과 N의 수가 같아지고 결국 사이클이 형성됩니다. 이제 간선의 가중치에 따라 정점의 가중치값을 만들지 못하는 경우가 발생합니다.

위와 같은 경우 가중치값을 어떻게 바꿔도 정수로 만들 수 없습니다. 이런 경우 No를 출력해 주어야 합니다. 즉 No가 나오는 경우를 체크하는 로직을 추가해 주어야 합니다.
마지막 간선의 가중치는 노드가 홀수개인지, 짝수개인지에 따라 계산하는 공식이 다릅니다. 왜냐햐면 x의 부호가 계속 바뀌기 때문입니다. 서브테스크2에서 A는 부호가 +, B는 부호가 -, C는 부호가 +, D는 부호가 -였습니다. 즉 홀수번째는 +, 짝수번째는 -부호이기 때문에 식이 바뀔수밖에 없습니다. 즉 마지막 가중치에 따라서 식이 이렇게 바뀝니다.
- 홀수일 때 : x + (k + x) = c
- 짝수일 때 : x + (k - x) = c
이 식을 풀어쓰면 다음과 같습니다.
- 홀수일 때 : 2x + k = c → x = (c - k)/2
- 짝수일 때 : x - x + k = c → k = c
마지막 값을 비교해서 No를 출력해야 하는 경우를 추가해 보겠습니다.
dfs 함수 만들기
cost = [0] * (N+1)
weight = [0] * (N+1)
impossible = False
INF = float("INF")
new_x = -INF
def dfs(node, node_cost, a):
global impossible, new_x
if cost[node]:
curr_a, curr_cost = cost[node]
if curr_a == a:
if curr_cost != node_cost:
impossible = True
else:
if (node_cost - curr_cost) % 2 == 1:
impossible = True
else:
new_x = curr_a * (node_cost - curr_cost) // 2
return
cost[node] = (a, node_cost)
weight[node] = -a * node_cost
for nxt, edge_cost in arr[node]:
dfs(nxt, edge_cost - node_cost, -a)
return
변경된 dfs 함수에서는 visited 리스트가 빠졌습니다. visited 리스트는 한 번 방문한 노드를 방문하지 않게 하기 위해 만든 것입니다. 하지만 서브테스크5에서는 사이클이 형성 되어 있기 때문에 한 번 방문한 노드라도 사이클 확인을 위해 방문을 해야합니다. 따라서 visited 리스트 대신 cost 리스트를 visited를 대신합니다. cost 리스트는 해당 노드를 방문 했을 때 데이터가 생성됩니다. 따라서 데이터가 있다면 사이클을 확인하는 로직을 추가하는 것입니다.
먼저 cost를 확인해서 데이터가 있는 경우 curr_a와 a값이 같은지 확인합니다. 해당 값이 같다면 노드가 짝수개 있다는 것을 알 수 있습니다.
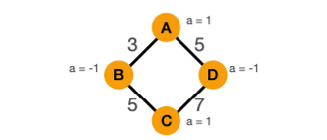
A 노드의 a값은 1입니다. B, C, D 노드로 이동하면서 a 값이 -1, 1, -1로 바뀌면서 A의 노드 a와 같은 1이 됩니다.

짝수가 아닌 홀수일 경우에는 A, B, C를 지나 다시 A로 돌아왔을 때 A의 a값과, 현재 a값이 달라질수밖에 없습니다.
curr_a와 a가 같다면 노드의 수가 짝수이기 때문에 k값과 c값이 같은지 확인한다고 했습니다. 따라서 curr_cost와 node_cost값을 비교하여 두 값이 다를 경우는 No를 출력해야 합니다. No를 출력하기 위해서 impossible이라는 변수를 만들어주었습니다.
if cost[node]:
curr_a, curr_cost = cost[node]
if curr_a == a:
if curr_cost != node_cost:
impossible = True
curr_a와 a가 다르다면 노드의 수가 홀수입니다. 노드가 홀수개 일때는 x값이 정해져 있습니다. 위에서 계산한 (c - k)/2 가 바로 x 값 입니다. 먼저 x값이 정수인지 아닌지부터 확인을 합니다. node_cost - curr_cost값을 2로 나누어 주는 것으로 x값이 정수인지 아닌지 확인할 수 있습니다. 나눈 값이 1일 경우 홀수이기 때문에 No를 출력합니다. 짝수일 경우에는 해당 값이 우리가 찾던 x값이기 때문에 new_x로 지정해 둡니다.
if (node_cost - curr_cost) % 2 == 1:
impossible = True
else:
new_x = curr_a * (node_cost - curr_cost) // 2
그럼 dfs함수 결과를 가지고 출력하는 부분을 수정해 보겠습니다.
결과 출력 수정하기
dfs(1, 0, 1)
if impossible:
print("No")
else:
if new_x != -INF:
x = new_x
else:
weight.sort()
x = weight[(N+1) // 2]
print("Yes")
for a, c in cost[1:]:
print(a * x + c, end=" ")
print()
impossible일 경우 No를 출력합니다. 다음으로 new_x가 존재하는 경우 x값을 new_x로 지정해 줍니다. new_x가 없는 경우는 이전 로직 그대로 동작하도록 합니다.
서브테스크6
서브테스크 6과 7은 같이 해결해 보도록 하겠습니다. 서브테스크5에서는 사이클이 하나였습니다. 그것도 처음과 끝이 연결된 사이클이였습니다. 하지만 서브테스크6, 7 에서는 사이클이 어디에 있는지 모르고, 몇 개의 사이클이 있는지도 모릅니다. 따라서 앞서 서브테스크5에서 구했던 new_x가 여러개가 될 수 있다는 것입니다.

위와 같이 ABCD에서 사이클이 생기고, EFGH에서 또 사이클이 생길 수 있는 것입니다. 위에서는 사이클의 노드 갯수가 짝수이기 때문에 new_x가 정해지지 않지만 홀수일 경우 new_x가 두 개 생기게 됩니다. 하지만 x값은 여러개일 수 없습니다. 따라서 여러곳의 new_x값이 모두 같을 경우만 Yes가 되고, 다를 경우에는 No가 됩니다.
따라서 new_x라는 set를 만들어 줍니다. set는 중복을 허용하지 않습니다. 사이클 마다 발견되는 new_x값을 더해주어 최종적으로 new_x값이 하나만 있다면 허용되고, 한 개 이상이라면 No를 출력해 줍니다.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**5)
N, M = map(int, input().split())
arr = [[] for _ in range(N+1)]
for _ in range(M):
a, b, c = map(int, input().split())
arr[a].append((b, c))
arr[b].append((a, c))
cost = [0] * (N+1)
weight = [0] * (N+1)
impossible = False
INF = float("INF")
new_x = set()
def dfs(node, node_cost, a):
global impossible, new_x
if cost[node]:
curr_a, curr_cost = cost[node]
if curr_a == a:
if curr_cost != node_cost:
impossible = True
else:
if (node_cost - curr_cost) % 2 == 1:
impossible = True
else:
tmp_x = curr_a * (node_cost - curr_cost) // 2
new_x.add(tmp_x)
return
cost[node] = (a, node_cost)
weight[node] = -a * node_cost
for nxt, edge_cost in arr[node]:
dfs(nxt, edge_cost - node_cost, -a)
return
dfs(1, 0, 1)
if 1 < len(new_x) or impossible:
print("No")
else:
if new_x:
x = new_x.pop()
else:
weight.sort()
x = weight[(N+1) // 2]
print("Yes")
for a, c in cost[1:]:
print(a * x + c, end=" ")
print()
기존 로직과 다른 점은 new_x라는 set을 만들고, new_x가 한 개일 경우만 허용되도록 하였습니다.
서브테스크 7
실제 정보 올림피아드 대회에서 출제하면 맞을수도 있지만 백준에서 제출 시 서브테스크7을 통과하지 못합니다. 이는 파이썬의 속도가 느리기 때문에 발생한 문제로 dfs함수를 재귀가 아닌 큐를 사용한 형태로 바꿔주어야 합니다. 여러 방법을 써봤는데 재귀로는 통과하지 못해 bfs로 바꿔 제출하였더니 100점을 맞을 수 있었습니다.
import sys
from collections import deque
input = sys.stdin.readline
N, M = map(int, input().split())
arr = [[] for _ in range(N+1)]
for _ in range(M):
a, b, c = map(int, input().split())
arr[a].append((b, c))
arr[b].append((a, c))
cost = [0] * (N+1)
weight = [0] * (N+1)
impossible = False
INF = float("INF")
new_x = set()
def bfs(node, node_cost, a):
q = deque()
q.append((node, node_cost, a))
while q:
node, node_cost, a = q.popleft()
if cost[node]:
curr_a, curr_cost = cost[node]
if curr_a == a:
if curr_cost != node_cost:
return True
else:
now_cost = node_cost - curr_cost
if now_cost % 2 == 1:
return True
else:
tmp_x = curr_a * now_cost // 2
new_x.add(tmp_x)
continue
cost[node] = (a, node_cost)
weight[node] = -a * node_cost
for nxt, nxt_cost in arr[node]:
q.append((nxt, nxt_cost - node_cost, -a))
return False
impossible = bfs(1, 0, 1)
if 1 < len(new_x) or impossible:
print("No")
else:
if new_x:
x = new_x.pop()
else:
weight.sort()
x = weight[(N+1) // 2]
print("Yes")
for a, c in cost[1:]:
print(a * x + c, end=" ")
print()
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 28219] 2023 정올 1차 주유소 (1) | 2023.08.23 |
|---|---|
| [백준 1655] 가운데를 말해요 (0) | 2023.08.22 |
| [백준 28326] 2023 정올 고기파티 (0) | 2023.08.21 |
| [백준 25402] 2022 정올 트리와 쿼리 (0) | 2023.08.18 |
| [백준 21762] 2021 정올 공통 부분 수열 확장 (0) | 2023.08.15 |



