[백준 20188] 등산 마니아
등산 마니아(20188)
문제 출처 : https://www.acmicpc.net/problem/20188
이 문제는 2020년 정보올림피아드 2차 대회 초등부 3번, 중등부 2번 문제 입니다.
문제 이해하기
한 번만 읽어서는 잘 이해하기 힘든 문제 입니다. 특히나 다양성이라는 용어가 중요한데 이 말의 뜻이 어렵습니다.
다양성은 길에 포함된 오솔길의 개수로 정의된다.
이렇게 정의 되어 있습니다. 문제를 제대로 읽지 않으면 다양한 경로의 개수로 잘못 이해하기 쉽습니다. 문제를 잘 읽어보면 이 문제에서 원하는 다양성은 두 지점을 지나는 간선의 개수 입니다. 이 간선의 개수는 최단 경로를 뜻하는 것이 아니라 정상 즉 루트를 지나는 경로입니다.

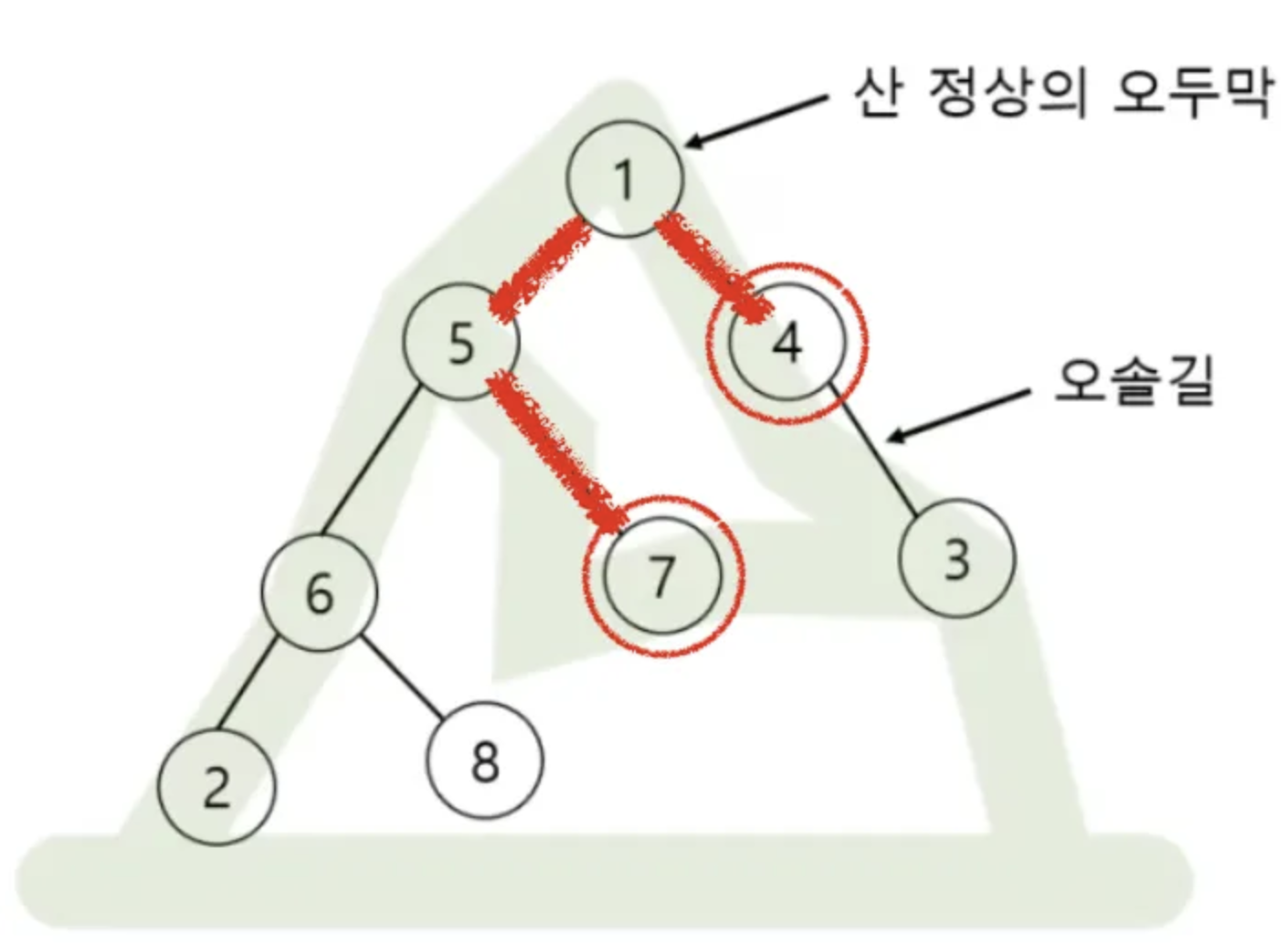
위와 같이 6, 7을 연결하는 다양성은 루트 부터 각 번호까지 간선의 개수 3개 입니다. 두 점을 선택 했을 때 각 간선들이 몇 번이나 선택되는지 계산하면 되는 문제 입니다.
5와 6을 연결하는 간선이 몇 번 선택 되는지 생각해 보겠습니다. 하나의 노드를 2, 6, 8번을 선택하면 다른 어떤 노드를 선택하더라도 5 와 6을 연결하는 간선이 사용됩니다. 위 그림 같이 6, 7 노드를 선택해도 루트인 1번과 연결되기 때문에 해당 간선이 선택되고, 6, 8을 선택해도 루트를 올라갔다 오기 때문에 해당 노드가 사용됩니다.

2, 6, 8번 노드 외에 다른 두 점을 선택하면 해당 간선이 사용되지 않습니다.
전체의 노드 사용 개수에서 1, 3, 4, 5, 7의 노드를 선택한 개수를 빼면 5, 6의 간선이 사용된 개수를 알 수 있습니다. 이렇게 모든 간선의 사용 개수를 구하면 다양성의 총합을 구할 수 있습니다.
코드 작성하기
그럼 코드를 작성해 보겠습니다
입력 받기
from collections import defaultdict
import sys
input = sys.stdin.readline
N = int(input())
arr = defaultdict(list)
for _ in range(N - 1):
u, v = map(int, input().split())
arr[u].append(v)
arr[v].append(u)
전체 오두막의 개수 N을 입력 받습니다. 다음으로 N - 1개의 노드 정보를 받아 그래프를 구성합니다. sys.stdin.readline을 input으로 하여 입력이 많더라도 빠르게 입력 받을 수 있게 하였습니다. 그리고 평소와는 다르게 노드 정보를 이차 리스트가 아닌 딕셔너리로 하였습니다. 딕셔너리로 하면 전체의 리스트를 만들어 놓지 않기 때문에 메모리를 좀 더 아낄 수 있습니다.
트리 구성
parent = [0] * (N + 1)
tree_cnt = [1] * (N + 1)
def dfs(start):
stack = [start]
dfs_order = []
while stack:
node = stack.pop()
dfs_order.append(node)
for child in arr[node]:
if child == parent[node]:
continue
parent[child] = node
stack.append(child)
while dfs_order:
node = dfs_order.pop()
tree_cnt[parent[node]] += tree_cnt[node]
dfs(1)
dfs로 트리를 구성하는 부분 입니다. 원래는 기본적인 dfs로 구성하였습니다. 하지만 이렇게 하니 메모리 초과가 발생하여 이렇게 구성하였습니다. 다른 풀이를 보면 C, C++, Java등은 단순한 dfs로 하였는데 파이썬에서는 재귀를 사용하면 메모리 초과가 발생합니다.
문제의 핵심은 각 하위 노드가 몇개나 있는지 알고 싶은 것입니다. 하위 노드의 개수를 알기 위해서 BFS를 사용할 수는 없습니다. 말단 노드까지 재귀를 통해 들어갔다가 올라오면서 개수를 구해야 하는데 BFS는 루트부터 계산하기 때문에 이 문제와는 맞지 않습니다.
dfs 알고리즘을 스택으로 구현하기 위해 각 노드들의 부모 노드를 구해주었습니다. parent 리스트에 각 노드들의 부모 노드가 저장 됩니다.
그리고 dfs_order 라는 리스트에는 dfs로 탐색할 때 사용되는 노드 정보를 저장합니다. dfs_order 리스트에서 pop을 사용하면 dfs와 같은 형태로 탐색을 할 수 있습니다.
tree_cnt에는 노드의 개수가 저장되어 있습니다. 초기에는 자기자신의 개수인 1개를 모든 노드가 가지고 있습니다. 그리고 부모 노드에 자식 노드의 개수를 더해줍니다. 그럼 루트 노드부터 말단 노드까지 자식 노드가 몇 개 인지 알 수 있습니다.
조합의 개수
ans = 0
def combi2(n):
return n * (n - 1) // 2
total_cnt = combi2(N)
for i in range(2, N + 1):
node_cnt = N - tree_cnt[i]
ans += total_cnt - combi2(node_cnt)
print(ans)
combi2 함수는 모든 노드에서 두 개의 노드를 선택했을 때 조합의 개수를 계산합니다. 전체 조합에서 각 노드의 조합 개수를 빼면 해당 위치의 간선이 몇 번 사용되었는지 알 수 있습니다. 이 값을 모두 더해주면 문제에서 요구하는 다양성의 개수를 알 수 있습니다.
전체 코드
전체 코드를 알아보겠습니다.
from collections import defaultdict
import sys
input = sys.stdin.readline
N = int(input())
arr = defaultdict(list)
for _ in range(N - 1):
u, v = map(int, input().split())
arr[u].append(v)
arr[v].append(u)
parent = [0] * (N + 1)
tree_cnt = [1] * (N + 1)
def dfs(start):
stack = [start]
dfs_order = []
while stack:
node = stack.pop()
dfs_order.append(node)
for child in arr[node]:
if child == parent[node]:
continue
parent[child] = node
stack.append(child)
while dfs_order:
node = dfs_order.pop()
tree_cnt[parent[node]] += tree_cnt[node]
dfs(1)
ans = 0
def combi2(n):
return n * (n - 1) // 2
total_cnt = combi2(N)
for i in range(2, N + 1):
node_cnt = N - tree_cnt[i]
ans += total_cnt - combi2(node_cnt)
print(ans)