2022년 정보올림피아드 필기 중등부(11 ~ 15)
2022년도 정보올림피아드 1차대회 필기 중등부 11번부터 15번까지 문제 풀이 입니다.
이전 문제는 아래 링크 확인 바랍니다.
2024.04.20 - [알고리즘 설명/정보올림피아드 필기] - 2022년 정보올림피아드 필기 중등부(1 ~ 5)
2024.04.21 - [알고리즘 설명/정보올림피아드 필기] - 2022년 정보올림피아드 필기 중등부(6 ~ 10)
11번

2310을 소인수분해하여 세 수를 만들 수 있습니다.
2310 = 2 * 3 * 5 * 7 * 11
위와 같이 표현할 수 있습니다. 이것을 적절히 분배하여 a, b, c의 경우의 수를 구하면 되는 문제 입니다.
a 가 1인 경우
먼저 a 가 1인 경우를 생각해 보겠습니다. a가 1이라면 b와 c로 2310이 될 수 있는 경우의 수 입니다. b를 4개의 숫자를 곱한 결과, c를 나머지 하나라고 하면 조합을 통해 구할 수 있습니다.
$$ _5C_4 = \frac{5 * 4 * 3 * 2}{4 * 3 *2 * 1} = 5 $$
다음으로 b가 3개의 숫자를 곱한 결과라고 한다면 다음과 같이 구할 수 있습니다.
$$ _5C_3 = \frac{5 * 4 * 3}{3 *2 * 1} = 10 $$
b가 2개의 숫자를 곱한 결과는 위에서 구한 c와 같습니다. 따라서 b가 2개인 경우는 계산하지 않아도 됩니다.
a, b가 소수 하나인 경우
다음으로 a와 b가 2, 3, 5, 7, 11 중 하나인 경우 입니다. c는 5개의 숫자 중 3개의 곱으로 되어 있습니다. 위에서 구한 5C3의 조합과 같기 때문에 10개의 경우가 나옵니다.
a, b가 소수 두 개의 곱인 경우
a가 2, 3, 5, 7, 11 중 2개의 수의 곱입니다. 이것은 5C2로 구할 수 있습니다. 10이 됩니다. b는 a가 고른 수를 빼고 3개 중 2개의 수를 고릅니다. 3C2로 3가지가 나옵니다. c는 나머지 하나를 가지면 됩니다.
a가 10가지 경우의 수, b가 3개의 경우의 수를 가지기 때문에 총 10 * 3으로 30가지의 경우의 수를 가집니다. a와 b가 중복되게 가질 수 있기 때문에 2로 나눈 15가지가 됩니다.
전체 합
이제 전체 합을 구하면 5 + 10 + 10 + 15로 40가지의 경우의 수가 나옵니다.
12번


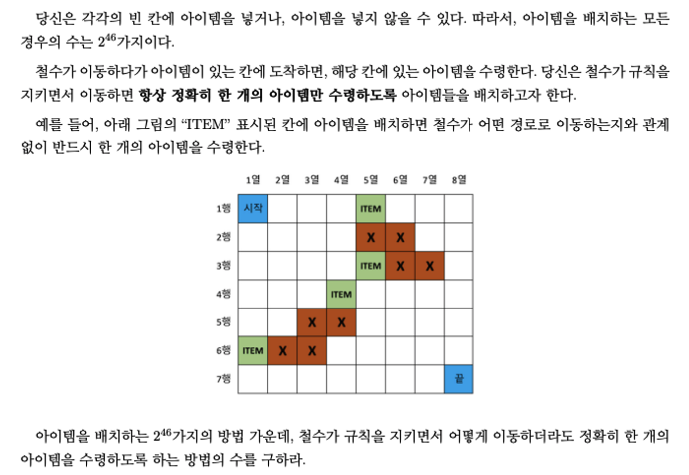
위 예제를 통해 어떤 경우 아이템을 얻을 수 있는지 알 수 있습니다. 철수가 이동할 수 있는 경로를 예상하여 무조건 한 개의 아이템을 얻을 수 있는 위치를 찾습니다. 경로를 잘못 선택하면 2개 이상의 아이템을 얻을 수 있기 때문에 하나의 경로만 얻을 수있게 합니다.
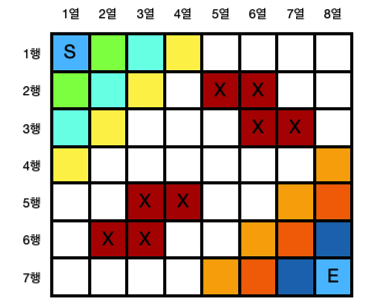
가장 먼저 생각할 수 있는 경로 입니다. 각 색깔에 아이템을 하나씩 놓으면 총 6개의 경우를 얻을 수 있습니다. S의 오른쪽과 아래에 있는 초록색을 생각해 보겠습니다. 초록색 두 칸만 칠해 놓으면 어떤 경로로 움직이던지 하나의 아이템을 얻을 수있습니다. 시작 위치 또는 도착 위치를 무조건 경유할 수밖에 없는 위치에 아이템을 놓은 것입니다.

다음으로 초록색쪽으로 이동한다면 초록색의 1번에서 6번 사이에 하나를 넣으면 됩니다. 노란색 쪽으로 이동한다면 1번부터 6번 사이에 하나를 놓으면 됩니다. 노란색 6번의 경우 경로가 두 개 이기 때문에 두 군데 모두 놓아야 합니다. 그리고 가운데로 이동한다면 에메랄드 색의 1번부터 회색의 6번까지 대각선으로 돌을 놓아야 합니다. 그럼 가운데 이동시 한번만 아이템을 만날 수 있습니다. 상단과 하단의 흰색 부분은 이미 위에서 체크한 것이기에 놓지 않았습니다. 이렇게 세 부분에 각각 6개의 경우로 아이템을 놓을 수 있기 때문에 6 * 6 * 6의 경우의 수를 가집니다. 여기까지 216의 경우의 수를 가지고 위에서 얻은 6개의 경우의 수로 총 222개의 경우의 수를 가지게 됩니다.
중간에 5행 2열, 6행 4열의 빈 부분이 보입니다. 이 두 자리에는 철수가 이동할 수 없는 곳입니다. 따라서 이곳에는 아이템을 놓아도 되고 놓지 않아도 됩니다. 2칸에 아이템을 놓는 경우의 수는 2 * 2로 4가지 입니다. 따라서 앞에서 구한 222개의 경우의 수에 4를 곱하면 총 888개의 경우의 수가 나오게 됩니다.
13번

초등부 13번 문제와 같습니다. 아래 링크를 통해 13번 확인 바랍니다.
https://davincicoding.tistory.com/133#13%EB%B2%88
2022년 정보올림피아드 필기 초등부(11 ~ 15)
2022년도 정보올림피아드 1차대회 필기 초등부 11번부터 15번까지 문제 풀이 입니다. 이전 문제는 아래 링크 확인 바랍니다. 2024.04.03 - [알고리즘 설명] - 2022년 정보올림피아드 필기 초등부(1 ~ 5) 202
davincicoding.co.kr
14번
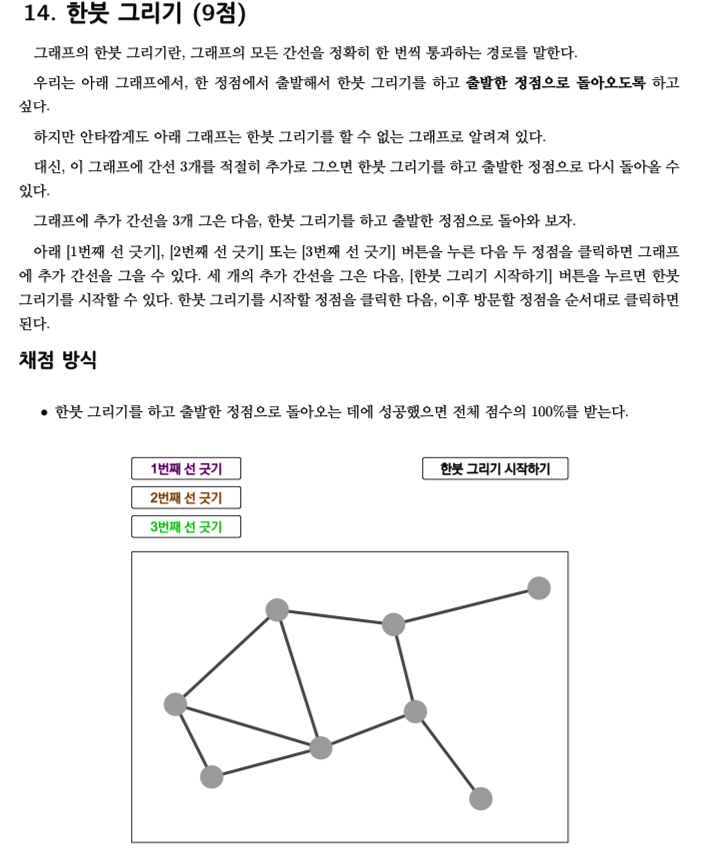
한 붓 그리기에 대해 정확히 이해하고 있어야 풀 수 있는 문제 입니다. 정점에 인접한 간선의 개수를 알면 한 붓 그리기가 가능한지 불가능한지 알 수 있습니다.
- 정점과 연결된 간선이 모두 짝수이면 한 붓 그리기를 어느점에서 시작해도 원래의 정점으로 돌아올 수 있습니다.
- 정점과 연결된 간선이 홀수인 점이 두 개 있으면 홀수점에서 시작하여 다른 홀수점으로 한붓 그리기를 할 수 있습니다.
- 홀수점이 2개보다 많다면 한 붓 그리기가 불가능 합니다.
여기서 원하는 것은 출발점으로 되돌아 오는 한 붓 그리기를 하고 싶어 합니다. 그럼 첫 번째 조건인 모든 정점이 짝수의 간선과 연결되어 있어야 합니다. 그럼 각 정점중 홀수인 정점을 찾아보겠습니다.

그림과 같이 6개의 점이 홀수의 간선으로 되어 있습니다. 3개의 간선을 추가하기를 원하니 간선들을 연결하면 모두 짝수로 만들 수 있고 한붓 그리기가 가능합니다. 아래는 한붓 그리기가 가능한 한 예 입니다.

15번

초등부 17번과 같습니다. 아래 링크를 통해 17번 확인 바랍니다.
https://davincicoding.tistory.com/134#17%EB%B2%88
2022년 정보올림피아드 필기 초등부(16 ~ 20)
2022년도 정보올림피아드 1차대회 필기 초등부 16번부터 20번까지 문제 풀이 입니다. 이전 문제는 아래 링크 확인 바랍니다. 2024.04.03 - [알고리즘 설명/정보올림피아드 필기] - 2022년 정보올림피아
davincicoding.co.kr