2020년 정보올림피아드 필기 중등부(11 ~ 2 - 3)
2020년도 정보올림피아드 1차 대회 중등부 필기 11번부터 2 - 3번까지 문제 풀이 입니다.
이전 문제는 아래 링크 확인 바랍니다.
2024.04.09 - [알고리즘 설명/정보올림피아드 필기] - 2020년 정보올림피아드 필기 중등부(1 ~ 5)
2024.04.11 - [알고리즘 설명/정보올림피아드 필기] - 2020년 정보올림피아드 필기 중등부(6 ~ 10)
11번

이렇게 초기 경우의 수가 나오는 문제는 DP로 출제되는 경우가 있습니다. 문제를 보면 피보나치 수열이 떠오르는 문제 입니다.
4를 만드는 경우를 생각해 보겠습니다. 4는 1을 만드는 경우에 3을 더해 만들 수 있습니다. 2에는 2를 더하고, 3에는 1을 더해주면 됩니다. 즉 4를 만드는 경우의 수는 1, 2, 3을 만드는 경우의 수의 합과 같습니다. 따라서 4를 만드는 경우의 수는 1 + 2 + 4로 7가지가 있습니다.
5를 만드는 경우는 2, 3, 4를 만드는 경우의 수의 합과 같습니다. 2 + 4 + 7로 위에서 말한 13가지라는 것을 알 수 있습니다.
6을 만드는 경우는 3, 4, 5를 만드는 경우의 수의 합입니다. 4 + 7 + 13으로 24입니다.
7은 7 + 13 + 24으로 44가 되고, 8은 13 + 24 + 44로 81이 됩니다.
12번

피보나치 수열 문제 입니다. 2 X 1의 타일을 채우기 위해서는 1개의 타일이 있으면 됩니다.
2 X 2 타일을 채우기 위해서는 2 X 1 타일을 채우는 방법에 세로로 하나 더 채우던가, 타일을 길게 늘여서 넣는 방법이 있습니다. 그렇게 2 X 2는 2가지 방법이 있습니다.
2 X 3은 2 X 1 타일에 길게 늘인 타일 두개를 연결하던가, 2 X 2 타일에 하나를 연결합니다. 즉 1 + 2가 되어 3가지 경우가 있습니다.
2 X 4는 2 X 2와 2 X 3의 합입니다. 따라서 2 + 3으로 5가 됩니다.
2 X 5는 3 + 5 로 8이 되어 결국 10까지 피보나치 수열의 값을 찾으면 되는 문제가 됩니다.
1 2 3 5 8 13 21 34 55 89
따라서 10번째 피보나치 수인 89가 정답이 됩니다.
2 - 1번
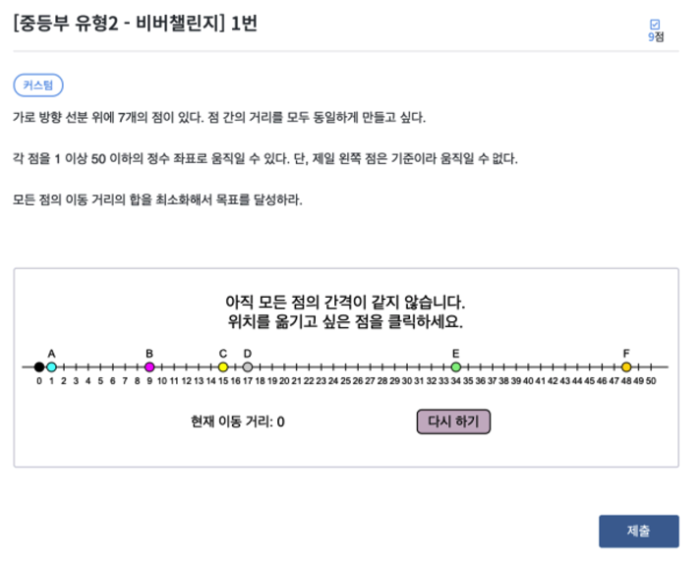
원점은 고정이기 때문에 총 6개의 점의 위치를 조절하여 가장 짧은 거리의 합을 구해야 합니다. 총 8개의 경우가 가능합니다. 왜냐하면 끝점이 50이기 때문에 6개의 점을 놓을 수 있는 최대값은 6 * 8 = 48 이라 점 간의 거리는 최대 8까지 만들 수 있습니다. 이를 8, 7, 6 순서로 줄여나가며 거리를 계산하면 6일 때 이동 거리가 34로 최소값을 구할 수 있습니다.

2 - 2번

초등부 2 - 1번과 같은 문제 입니다.
아래 링크에서 초등부 2 - 1번 확인 바랍니다.
https://davincicoding.tistory.com/123#2_-_1%EB%B2%88
2020년 정보올림피아드 필기 초등부(11 ~ 2 - 3)
2020년도 정보올림피아드 1차 대회 초등부 필기 11번부터 2 - 3번까지 문제 풀이 입니다. 이전 문제는 아래 링크 확인 바랍니다. 2024.03.24 - [알고리즘 설명] - 2020년 정보올림피아드 필기 초등부(1 ~ 5)
davincicoding.co.kr
2 - 3번

초등부 2 - 2번과 같은 문제 입니다.
아래 링크에서 2 - 2번 확인 바랍니다.
https://davincicoding.tistory.com/123#2_-_2%EB%B2%88
2020년 정보올림피아드 필기 초등부(11 ~ 2 - 3)
2020년도 정보올림피아드 1차 대회 초등부 필기 11번부터 2 - 3번까지 문제 풀이 입니다. 이전 문제는 아래 링크 확인 바랍니다. 2024.03.24 - [알고리즘 설명] - 2020년 정보올림피아드 필기 초등부(1 ~ 5)
davincicoding.co.kr