2022년 정보올림피아드 필기 초등부(1 ~ 5)
2022년도 정보올림피아드 1차대회 초등부 필기 문제 풀이 입니다.
1번

banana의 경우는 a가 3개 있기 때문에 다른 문자의 위치에 따라 사전순으로 배열할 때 신경써 주어야 합니다. 하지만 foobar 의 경우 a가 하나 있기 때문에 a만 맨 앞으로 이동시켜주면 됩니다. 따라서 arfoob가 사전에서 가장 먼저 나오고 이는 4개의 문자를 뒤로 옮겨주면 됩니다.
2번

위 문장에 기록된 두 가지는 사실 입니다. 첫 번째 P와 R 둘 중 한명은 케익을 먹었다는 사실을 알 수 있습니다. 그럼 두 번째에서 P가 케익을 먹지 않았다는 것은 R이 먹었다는 뜻과 같습니다. 즉 두번째 기록은 다음과 같이 바꿔 쓸 수 있습니다.
- R이 케익을 먹었거나, Q가 케익을 먹었다. R이 케익을 먹은 동시에 Q가 케익을 먹었을 수도 있다.
결국 이 문장은 Q나 R 둘 중 한명이 케익을 먹었거나, 둘 다 먹었다는 뜻이 됩니다. 따라서 정답은 2번이 됩니다.
3번

모자를 떨어뜨리고 10분이 지난 뒤에 반환점을 돌고, 모자를 잃어버린 것을 알게 되었습니다. 정확히 계산할 수도 있지만 이런 문제는 쉬운 형태로 바꿔서 계산하는 것이 좋습니다.
모자를 떨어뜨리고 한시간이 지났다고 해보겠습니다. 즉 12km를 이동해 온 것입니다. 모자역시 원래 위치에서 2km이동합니다. 이제 배가 한시간을 거슬러 올라가면 8km 를 이동합니다. 모자역시 배가 이동하는 한시간 동안 2km를 더 이동합니다. 결국 이동한 시간만큼 거슬러 올라가면 모자를 만날 수 있습니다.
따라서 이 문제에서 제시한 시간인 10분 후 모자를 만나게 됩니다.
4번

자신과 자신을 잇는 간선, 임의의 정점 쌍을 잇는 간선이 두 개 이상 있으면 안된다는 것은 아래 그림과 같습니다.
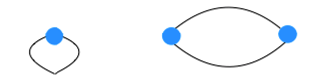
첫 번째 그림처럼 자신이 자신을 연결하면 안되고, 두 번째 그림처럼 같은 두 점에 대해 두개의 간선이 있으면 안됩니다.
먼저 정점의 차수의 합이 홀 수로 있을 수는 없습니다. 시작이 있으면 끝이 있기 때문에 정점의 차수의 합은 항상 짝수여야 합니다.
첫 번째와 세 번째는 정점의 차수의 합이 홀수 입니다. 따라서 하나의 제대로 간선이 연결되지 않았다는 뜻 입니다.
네 번째는 1번과 2번은 정점이 5개씩 연결되어 있습니다. 즉 자신을 제외한 모든 정점이 연결되어 있다는 뜻입니다. 하지만 마지막 6번 정점은 차수가 1입니다. 이 말은 1, 2번이 모든 정점과 연결이 되지 않았다는 뜻과 같습니다. 따라서 네 번째도 잘못 연결된 것입니다.
그럼 남은 2번은 차수의 합이 짝수라 문제가 없습니다. 각 정점과 연결된 간선을 제거한다고 해보겠습니다.
4 2 4 2 3 3
첫 번째 정점에서 4개의 간선을 없애면 나머지 정점중 4개의 정점에서 차수가 1씩 줄어 듭니다.
0 1 3 1 2 3
다음 세 번째 정점의 간선 3개를 없애보겠습니다.
0 1 0 0 1 2
여섯 번째 정점의 간선 두 개를 제거하면 모두 0이 되어 연결이 정상적이라는 것을 알 수 있습니다. 아니면 아래와 같이 차수에 맞는 그림을 그려보는 것도 방법 입니다.
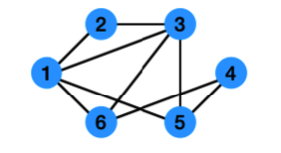
5번

9등인 영희가 2등급을 받기 위해서는 1등급이 8명일 경우 최대값이 됩니다. 그럼 9등부터 9명이 2등급이 됩니다. 즉 18등까지가 2등급입니다. 17등이 3등급이기 때문에 이는 맞지 않습니다. 따라서 최대값을 7로 바꿔 계산해 보겠습니다.
1등급이 7명 7등, 2등급은 8명 16등, 3등급은 9명 26등까지입니다. 따라서 조건에 모두 만족합니다.
이제 최소값을 생각해 보겠습니다. 영희가 2등급을 받기위한 최소값은 1등급이 4명일때 가능합니다. 1등급이 4명, 2등급이 5명으로 9등이 2등급이 됩니다. 하지만 3등급은 6명이기 때문에 16등까지만 3등급이 가능합니다.
그럼 최소값을 5명으로 생각해 보겠습니다. 1등급이 5명으로 5등, 2등급이 6명으로 11등까지 가능합니다. 3등급은 7명으로 18등까지 가능합니다. 마지막으로 4등급은 8명으로 26등까지 입니다. 미나가 4등급이 될 수 없기 때문에 최소값을 6으로 시도해 봅니다.
1등급이 6명 6등, 2등급이 7명 13등, 3등급이 8명 21등, 4등급이 9명 30등으로 모든 조건에 만족합니다. 따라서 정답은 2번 최소 6, 최대 7 입니다.