2021년 정보올림피아드 필기 초등부(11 ~ 15)
2021년 정보올림피아드 1차대회 초등부 11번부터 15번까지 문제 풀이 입니다.
2024.03.27 - [알고리즘 설명] - 2021년 정보올림피아드 필기 초등부(1 ~ 5)
2024.03.30 - [알고리즘 설명] - 2021년 정보올림피아드 필기 초등부(6 ~ 10)
11번

이렇게 회전을 하였을 때 겹치는 경우를 같은 형태로 보는 것을 원순열이라고 합니다. 그리고 조각을 뒤집을 수 없다는 것은 염주순열 혹은 목걸이 순열은 아니라는 뜻입니다.
그럼 먼저 원순열이 무엇인지부터 알아보겠습니다. 원탁이 있고 1번부터 4번까지 자리에 앉는다고 하겠습니다. 이 때 앉을 수 있는 경우의 수를 구하는 것입니다. 원탁에 1, 2, 3, 4순서로 앉아 있는 것과 4, 1, 2, 3순서로 앉아 있는 것은 같은 순서로 앉아 있는 것으로 보는 것 입니다.

이 두가지 방식은 원탁에 앉아 있는 사람의 입장에서 보면 똑같습니다. 1번은 3번을 마주보고 있고, 왼쪽에는 2번, 오른쪽에는 4번이 있습니다.
염주 순열은 여기에서 뒤집는 경우도 같은 경우로 보는 것입니다.

위와 같은 경우는 원순열 입장에서는 분명 다른 순열입니다. 왼쪽의 1번 입장에서 왼쪽이 2번이였는데 오른쪽에서는 오른쪽이 2번 입니다. 그러니 다르지만 이것이 목걸이의 배치라면 뒤집는 순간 두 경우는 같은 것입니다. 이것을 염주순열이라고 하고, 이 문제에서는 뒤집는 경우가 없다고 했으므로 염주순열인지 아닌지 고민할 필요가 없어진 것입니다.
위 문제는 결국 아래와 같은 원순열에서 사람이 자리에 앉을지 말지를 정하는 것과 같습니다. 이 때 사람을 구별하는게 아니라 앉은 사람이 있는지, 없는지만을 판단 합니다.

먼저 아무도 앉아 있지 않는 경우가 한 가지, 한 명만 앉아 있을 경우 한 가지가 있습니다.

파란색이 빈 자리이고, 초록색이 앉은 자리 입니다. 위 문제로 이해하려면 파란색이 오목한 부분이고, 초록색이 볼록한 부분이라고 이해해도 됩니다.
이제 두 사람이 앉을 경우를 생각해 보겠습니다.

위와 같이 세가지 경우가 있습니다. 이제 3명이 앉는 경우를 생각해 보겠습니다.
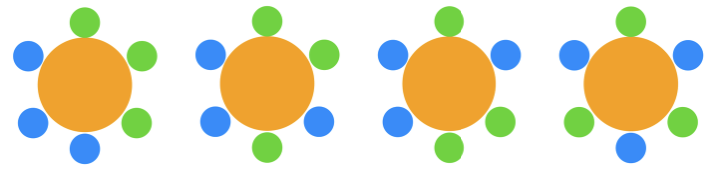
세 명이 앉을 다른 경우는 위와 같이 4가지 경우가 있습니다.
네 명이 앉을 경우는 위에서 두 명이 앉을 경우와 결국 같습니다. 네 명이 앉을 경우라는 것은 두 명이 앉지 않는 위치를 찾는것입니다. 이것은 두 명이 앉을 경우와 본질적으로 같습니다.
마지막으로 다섯 명이 앉을 경우 하나, 여섯명이 앉을 경우 하나가 존재합니다. 이것 역시 한명만 앉을 경우랑, 모두 앉지 않은 경우와 같습니다. 지금까지 구한 모든 경우의 수를 더하면 결과를 얻을 수 있습니다.
1 + 1 + 3 + 4 + 3 + 1 + 1 = 14
이렇게 4가지 경우를 찾았고 그 경우는 14개의 경우임을 알 수 있습니다.
12번

보기를 확인해보면 1번 3개를 제외하고는 숫자가 크다는 것을 알 수 있습니다. 딱 봐도 3개보다는 많은 사각형이 보이기 때문에 하나하나 세어보기 보다는 규칙을 찾아야 문제를 쉽게 해결할 수 있습니다. 최소 20개가 넘어가니 세어본 것을 또 셀수도 있고, 잘못 계산하기 쉽습니다.
왼쪽 상단을 기준으로 하여 사각형을 만들고 회전 여부를 따져보겠습니다. 아래 그림처럼 파란색 점에서 외부 육각형을 변으로 사용하지 않는 경우 입니다.
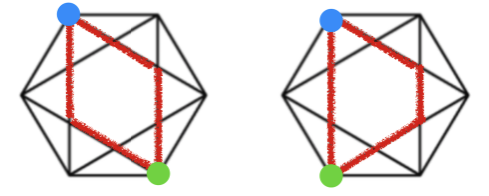
회전을 시켰을 때 왼쪽 그림은 대칭의 모양이 되어 파란색 점이 초록색 점의 위치에 왔을 때 똑같은 그림이 됩니다. 따라서 왼쪽과 같은 사각형은 3개가 있습니다. 반면 오른쪽 그림은 회전을 시켜보면 6단계로 회전이 됩니다. 따라서 총 6개의 사각형이 있다고 할 수 있습니다. 최종적으로 3 + 6으로 9개의 사각형이 있습니다.
다음으로 아래 그림과 같이 좌측 상단의 변을 공유하는 사각형 입니다.

왼쪽 그림은 회전시 똑같은 그림이 되는 경우가 있으므로 3번, 오른쪽 두 그림은 회전해도 같은 그림이 나오지 않으므로 6개씩 12개 입니다. 따라서 좌측 상단의 변을 공유하는 사각형은 3 + 6 + 6로 15개 입니다.
좌측 상단, 중앙 상단의 변을 공유하는 삼각형 입니다.

이 사각형을 회전해도 겹치는 경우가 없기 때문에 6개의 사각형을 가집니다. 바깥 정 육각형의 외곽 변 4개를 공유하는 사각형은 만들 수 없기 때문에 더 이상 사각형을 만들 수 없습니다.
처음 9개, 두 번째 15개, 마지막 6개를 계산하면 총 30개의 사각형을 찾을 수 있습니다.
13번

직접 시뮬레이션을 통해 좌석을 정할 수 있습니다. 이런 문제는 쉬운 규칙부터 하나하나 해결하면 됩니다. 먼저 가장 쉬운 규칙인 4번을 보겠습니다. D는 E 바로 오른쪽에 앉습니다. 따라서 아래와 같이 표현할 수 있습니다.
E D
다음으로 규칙3을 보면 B, C는 E의 바로 옆에 앉을 수 없습니다. 이미 E의 오른쪽은 D 이기 때문에 남은 A가 E의 왼쪽이 됩니다.
A E D
다음 규칙 2로 인해 A, B는 D 바로 옆에 앉을 수 없습니다. A의 위치는 이미 정해졌기 때문에 B의 위치를 D와 떨어진 A 옆으로 옮기면 됩니다.
B A E D
마지막으로 C는 A, B의 바로 옆이 될 수 없습니다. 따라서 C의 위치를 D의 옆으로 옮겨주면 됩니다.
B A E D C
그럼 위와 같이 표현이 되고, 이것을 선분으로 이어주면 아래 그림과 같이 그려줄 수 있습니다.

14번

어떤 암호를 암호화 한 뒤 복호화 하는 과정은 거꾸로 진행하면 됩니다. 즉 암호를 2단계롤 먼저 풀고, 다시 1단계로 풀게 되면 문장을 해독할 수 있습니다. 먼저 2단계를 거꾸로 변환하여 보겠습니다. 암호를 기준으로 표에 작성을 하면 아래와 같이 됩니다.
2 4 1 3 5
| L | K | G | Y | L |
| L | K | L | L | G |
| N | G | N | Y | N |
| K | K | Y | Y | Y |
| Y | N | Y | N |
다음으로 이 문장을 가지고 1단계 변환을 진행 합니다.
LK GY LL KL LG NG NY NK KY YY YN YN
LK는 3을 나타냅니다. 다음 GY는 M을 나타냅니다. 이런 방식을 사용하여 문장을 찾으면 아래와 같은 문장을 찾을 수 있습니다.
3MAT4CUPFREE
15번

넣기를 통해 스택에 넣고, 뽑기를 통해 정렬을 해야 합니다. 문제는 제거하기를 통해 잘못된 배열을 바로잡아야 합니다. 정렬을 하기 위해서는 스택에 이전 숫자보다 작아지는 숫자를 넣어야 합니다. 그리고 뽑기를 할 때에는 커지는 순서대로 꺼내야 합니다.
넣고 빼기를 하는데 처음에는 8이 있고, 다음에는 8보다 작은 5가 있고, 다음은 5보다 작아야 합니다. 하지만 그보다 큰 6이 있어 스택을 정렬 시킬 수 없습니다. 따라서 6을 제거해야 한다는 것을 알 수 있습니다. 하지만 문제를 잘 보면 7번째의 3보다 8번째의 7이 더 큽니다. 이 경우도 잘못된 것 같지만 뽑기를 통해 1부터 5까지 정렬을 시킬 수 있기 때문에 문제 없습니다. 남은 8이 7보다 크기 때문에 문제가 없습니다.
계산이 어렵다면 순서대로 넣기를 하다 1부터 정렬이 되는 순서대로 뽑기를 하다보면 6에서 문제가 생기는 것을 알 수 있습니다. 따라서 6을 제거하는 방향으로 다시하기를 해도 됩니다.
그럼 다음과 같이 진행하면 문제를 해결할 수 있습니다.
넣기(8)->넣기(5)->제거(6)->넣기(1)->뽑기(1)->넣기(4)->넣기(2)->뽑기(2)->넣기(3)->뽑기(3)->뽑기(4)->뽑기(5)->넣기(7)->뽑기(7)->뽑기(8)->넣기(10)->넣기(9)->뽑기(9)->뽑기(10)