2020년 정보올림피아드 필기 초등부(2 - 4 ~ 2 - 8)
2020년도 정보올림피아드 1차 초등부 필기 문제 풀이 입니다.
2024.03.24 - [알고리즘 설명] - 2020년 정보올림피아드 필기 초등부(1 ~ 5)
2024.03.25 - [알고리즘 설명] - 2020년 정보올림피아드 필기 초등부(6 ~ 10)
2024.03.26 - [알고리즘 설명] - 2020년 정보올림피아드 필기 초등부(11 ~ 2 - 3)
2 - 4번

짧은 경로를 선택하다보면 쉽게 경로를 그릴 수 있습니다. 우선 이런 최단경로를 구하는 알고리즘은 다익스트라 알고리즘입니다. 하지만 다익스트라 알고리즘은 출발점과 도착점이 정해져 있습니다. 이렇게 출발점과 도착점이 정해지지 않았다면 플로이드 와샬 알고리즘을 사용합니다. 플로이드 와샬 알고리즘에 대해서는 아래 링크 확인 바랍니다.
03. 플로이드 와샬 알고리즘
# 플로이드 와샬 알고리즘 플로이드 와샬(Floyd Warshall) 알고리즘 역시 앞에서 알아 보았던 최단 경로 알고리즘 중 하나 입니다. 다익스트라 알고리즘은 출발점에서 모…
wikidocs.net
거리의 합이 짧은 경로로 계속 늘려나가면 됩니다.

짧은 거리만 선택하면 이와 같이 나타낼 수 있지만 한 장소를 두 번 이상 방문하게 됩니다. 한 장소를 한번만 방문하도록 거리를 계산하며 수정하면 아래와 같은 경로를 얻을 수 있습니다.

2 - 5번

선택 정렬을 통해 작은 숫자를 앞으로 이동시키면 오름차순으로 정렬이 가능 합니다. 선택 정렬은 아래 링크에서 확인 바랍니다.
https://wikidocs.net/205624#_1
02. 정렬
[TOC] 우리는 정렬을 정말 많이 사용하고 있습니다. 인터넷에서 게시글을 보더라도 최신순, 좋아요가 많은 순서대로, 댓글이 가장 많은 순서대로 등등 다양한 방식으로 정렬을 사…
wikidocs.net
먼저 가장 작은 숫자를 찾아 첫 번째 위치와 바꿔 줍니다. 12가 가장 작기 때문에 맨 앞에 위치한 20과 위치를 바꿔 줍니다.
12 15 28 20 19 27 31 16 21 30 24
두 번째로 작은 15는 이미 두 번째에 위치하고 있기 때문에 세 번째 작은 수를 찾습니다. 16을 3번째 위치인 28과 교환해 줍니다.
12 15 16 20 19 27 31 28 21 30 24
4번째 작은 수인 19를 20과 교환하여 줍니다.
12 15 16 19 20 27 31 28 21 30 24
5번째로 작은 20은 이미 정렬되어 있기 때문에 다음으로 작은 21을 6번째 위치에 있는 27과 교환 합니다.
12 15 16 19 20 21 31 28 27 30 24
7번째로 작은 24를 7번째 위치에 있는 31과 교환 합니다.
12 15 16 19 20 21 24 28 27 30 31
마지막으로 8번째로 작은 27을 8번째에 위치해 있는 28과 교환합니다.
12 15 16 19 20 21 24 27 28 30 31
이렇게 6번의 교환으로 모든 숫자를 오름차순으로 정렬할 수 있습니다.
2 - 6번

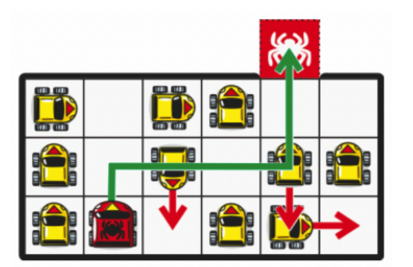
시뮬레이션을 통해 가장 짧은 거리를 생각해야 합니다. 아래와 같이 빨간 차가 이동 가능한 최소 횟수는 8번 입니다. 8번의 이동이 가능하도록 노란 차를 이동 가능한 횟수는 3번이기 때문에 총 11번의 이동이 필요합니다.
2 - 7번

가장 작은수를 만들고 싶지만 아무렇게나 옮겨서는 작은 수를 만들 수 없습니다. 작은 수를 만들기 위해서는 왼쪽에는 작은 숫자를, 오른쪽에는 큰 숫자가 배치 되도록 해야 합니다. 그러기 위해서 이전 숫자보다 크면 오른쪽으로, 작으면 왼쪽으로 배치한다면 작은 숫자를 만들 수 있을 것 같습니다.
9는 첫 숫자이니 오른쪽, 왼쪽 어디에 두어도 의미가 없습니다. 여기서는 오른쪽으로 두도록 하겠습니다. 그리고 다음 4는 9보다 작으니 왼쪽에 두도록 하겠습니다.

9, 4 다음 숫자들이 어디로 갈지 생각해 보겠습니다. 작은 숫자를 만들기 위해서는 앞으로 갈수록 작은 숫자가 와야 합니다. 따라서 왼쪽으로 갈 숫자는 노란색으로, 오른쪽으로 갈 숫자는 초록색으로 표시하였습니다. 맨 위에 있는 4는 8보다 작고, 3은 7보다 작고, 1은 4보다 작습니다. 그 외 초록색 색깔들은 위쪽에 있는 노란색보다 큰 숫자임을 알 수 있습니다.
이제 위의 숫자를 모두 옮기면 아래와 같은 결과를 얻을 수 있습니다.

2 - 8번

두 수열 q와 p가 같다면 차이의 합이 0이 됩니다. 따라서 배열의 칸을 교환해서 숫자가 작아진다면 q와 p가 비슷한 값으로 변하고 있다는 것이고, 숫자가 커진다면 달라진다는 뜻입니다. 따라서 교환을 통해 숫자가 점점 작아지는지를 확인해야 합니다.
교환의 횟수가 얼마가 되던지 상관 없기 때문에 계산하기 편하게 오름차순으로 정렬합니다. 1부터 11까지 위치에 맞게 이동시켜 줄 수 있습니다.
1 2 3 4 5 6 7 8 9 10 11
이렇게 이동하고 나면 차이의 합은 30이 됩니다. 이제 가장 큰 수인 11부터 위치를 찾습니다. 위치를 찾는 방법은 앞의 숫자들과 교환해 가면서 가장 숫자가 작은 경우를 찾는 것입니다. 숫자를 교환하여 작아지면 그대로 두고, 커지면 원래대로 돌리는것을 계속적으로 반복합니다.
이렇게 반복을 하다가 0이되는 순간이 두 수열이 같아진 것입니다.
귀찮은 반복이 많은 문제로 시간이 많이 남은 경우에만 시도하는 것이 좋습니다.